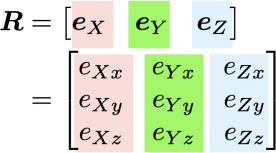モーションセンサを使用した角度の算出方法 その1
図1：モーションセンサを利用した角度計測
モーションセンサはクォータニオンを初め，オイラー角などの3次元の姿勢角度を出力します．しかし，モーションセンサからクォータニオンが出力されても，実際の角度計測にどのように利用したら良いかわからない方も多いかと思います．
例えば，骨格の線画（スティックピクチャ）の角度をする際に，クォータニオンからそのような角度を計算したいことがあると思いますが，ここではその考え方をご説明いたします．モーションセンサからスティックピクチャを描く際にも，この考え方は役立つはずです．
3次元の姿勢角度の基礎
まず，様々な角度算出を行いたい方のために，その数学的基礎について述べていきます．
なお，最終的な計算方法の結果は次のページで示しますので，以下は読み飛ばしていただいても結構です．
角度と回転
「姿勢」について説明する前に，改めて「角度」と「回転」について整理をしておきたいと思います．
直線の幾何学
剛体の幾何学
回転と角度
図2：直線と平面の幾何学
図3：3次元直交座標系による剛体の姿勢角度
図4：二つの座標系間の回転
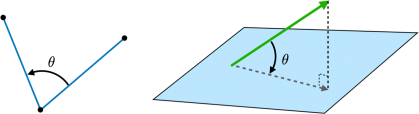
3次元空間では「二直線のなす角度」や「直線が平面となす角度」などが例としてあげられます．このような角度を定義するためには，点や線や面が登場しますが，「直線が平面となす角度」も最終的には図の緑色の線と，平面に投影された直線間の角度であって，基本的には「二つの直線のなす角度」をイメージしていただくと良いと思います．
そして，移動対象である「直線」は同じ向きの「一つの軸」として表現されます．この「一つの軸」の意味は，次の剛体との対比で意味が明確になると思います．
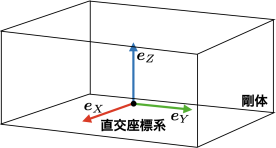
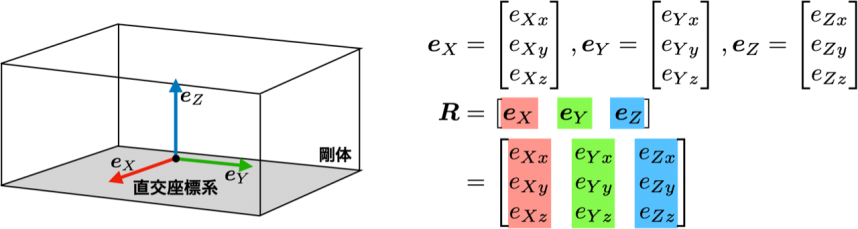
剛体とは形が変化しない物体を意味します．そして「剛体の幾何学」における角度を表現するためには，図3のように剛体に「直交座標系」すなわち「三つの軸」が張り付いている状態をイメージしてください．
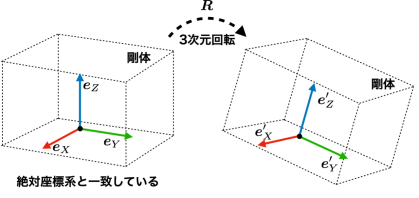
では「角度」とは何か？を考えると，直線や剛体などの「対象」を「回転」させて，異なる「対象」と一致させるような「回転運動を与えた」際の回転量と，ここでは考えることにします．このような考え方に立つと，「二直線のなす角度」は図2に示したように「ある直線が異なる直線に対して，方向を一致させるような回転運動を与えた際の回転量」を，「剛体の姿勢角度」は図4に示すように「ある剛体が異なる剛体に対して，軸方向を一致させるような回転運動を与えた際の回転量」を，指します．
姿勢角度から，二直線のなす角度へ
「姿勢」または「姿勢角度」とは，剛体に限定された回転量（角度）を表す際に使用する用語で，「二つの異なる方向を向いた剛体の直交座標系を一致させる回転量」を指します．英語ではorientation，またはattitudeなどとも呼びます．また，単に「剛体の姿勢角度」と述べる場合は，暗黙のうちに絶対座標系などのような比較する基準とする座標系が存在し，その基準座標系と剛体に固定された座標系間の回転角度を指しています．
そして，モーションセンサは「剛体の姿勢角度」としてクォータニオンやオイラー角を出力します．
一方，「関節の可動域」「センサの水平面となす角度」「二つのセンサ（腕と腕の）のなす角度」「腕の進展・屈曲角度」などは，前述の「直線の幾何学」における「二直線のなす角度」に相当します．
すると，例えば，『どのようにクォータニオンから「二直線のなす角度」をどのように計算できるのか？』が，ここでの課題になり，三つの軸から一つの軸を抽出し，その回転量を計算する方法が具体的な方法となります．
そこで，次にクォータニオンを利用して，「直線が平面となす角度」などを計算する方法の基礎的な説明をします．
剛体の姿勢角度
「回転行列」＝「直交座標系の各軸に固定された単位ベクトル（基底）」
繰り返しになりますが，剛体の姿勢は，剛体（変形しないと見なされた物体）に三つの軸が固定されている状態をイメージし，「剛体の姿勢角度」＝「直交座標系の回転」と捉えてください．
したがって，この直交座標系を定義する，最も基本は，三つの直交する座標軸に固定されたベクトルとなります．そのうち，長さ（大きさ・ノルム）が1のベクトルを単位ベクトルと呼びますが，各座標軸に固定された三つの直交する単位ベクトルの組み合わせを，基底と呼びます．そこで，
式(1)
のように基底をeX, eY, eZと定義すると，これらは直交しているので，異なる二つの基底同士の内積は0となります．同じ基底同士の内積は，それぞれは単位ベクトルですから1になります．
なお，この式では少し見にくいのですが，太字・イタリック書体の e と，イタリック書体の e と区別され，前者の太字・イタリック書体はベクトルを意味して，スカラーやベクトルの要素であるイタリック書体の記号と区別しています．1行目の最初の式は，座標系のX軸に固定された単位ベクトルをeXを表していて，その右辺は縦ベクトル（要素を縦に並べたベクトル）で，そのeXの各成分を，絶対座標系のxyz成分（e_Xx, e_Xy, e_Xz）で記述したものです．ここで大文字のXYZは物体に「固定されたローカル座標系」を意味して，小文字のxyzは「絶対座標系」を表しています（図5参照）．
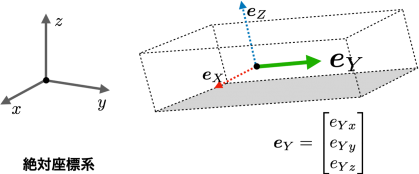
例えば，図4の左のように，もし剛体に固定された単位ベクトル eYが絶対座標系のy軸と一致している場合は，eY=[0,1,0]^T となります．それぞれeX, eY, eZのベクトルは直交していて，それぞれ絶対座標系の中における，各単位ベクトルの方向を大きさ1のベクトルで表現しています．ここで^T は横ベクトル（[a,b,c]のように横に並べたベクトル）を縦ベクトル（a,b,cを縦に並べたベクトル．上のeYの式で示したような並べ方）に変換する転置（Transpose）記号です．紙面のスペースの関係でこのように記述しています．
回転行列の定義
そして実は，これらの「基底を並べたもの」が回転行列 Rに相当します．なお，2次元でも3次元でも回転行列は，一般的には三角関数を利用して導入されることが多いと思いますが，こちらの導入の仕方の方が，より回転行列の意味を捉えやすいはずです．もちろん，三角関数の回転から導出された回転行列と完全に一致します．
このことから回転行列は，「各基底（各軸の単位ベクトル）の絶対座標系（または他の基準座標系）への射影，または方向余弦」を，並べた行列とも言えます．
例：Y軸の姿勢
クォータニオンとの関係が不明でも，剛体の姿勢角度とは剛体に固定された直交座標系の三つの軸の方向に相当するという事実から，たとえば，「センサのY軸と棒の長軸を一致させた剛体の，長軸方向がわかれば，望みの角度を計算できる」予感がします．
図5：回転の例（Y軸に注目）
さて，図4の左の状態から，図5のように回転させたときの剛体のY軸 eY の単位ベクトルの要素を，ここでは絶対座標系のxyz成分（e_Yx, e_Yy, e_Yz）で表していて，
回転行列 R の真ん中の eY がそれに相当しています．つまり直線を表す「一つの軸」が，回転行列の中に含まれています．
姿勢の表現方法（回転行列・オイラー角，クォータニオン）
このように，「3次元姿勢の基本の表現方法は基底を並べた回転行列」です．基本という意味では，オイラー角でもクォータニオンでもありません．オイラー角やクォータニオンの変換も，「必ず回転行列を経由しないと計算できない」からです．
しかし，3次元の姿勢角度というと，もっと少ないパラメータで表現するイメージをお持ちの方も多いと思います．確かに回転行列は姿勢表現としては，9個のパラメータを使っているので，多過ぎ（冗長）です．
実は，9個のパラメータは単位ベクトルで表現しているので冗長ですが，「直交条件」3個と，「単位ベクトルの大きさが1という条件」3個を消すことができ，3個のパラメータまで減らすことが可能です．
そこで，最小の3個のパラメータで姿勢角度を表現する方法がオイラー角で，冗長ですが4個のパラメータで表現する方法がクォータニオンです．これらの詳細については「オイラー角による姿勢表現」や「クォータニオンによる姿勢表現」をご参照ください．なお，9個はさすがに多過ぎですが，クォータニオンやオイラー角から，直感的に回転量を捉えるのが難しいと言うことで，二つの軸で表現する方法もあります．ここでは詳しく述べませんが，有顔ベクトルと呼ばれる方法で，残った一つの軸は直交条件（具体的には外積を使用して）からすぐに計算できるので，冗長ですが6個のパラメータで表現する方法もあります[1, 2]．
ここでは，オイラー角やクォータニオンの詳細を理解できなくても構いません．まずは，姿勢，すなわち座標系の基底（各軸に固定された単位ベクトル）の幾何学的なイメージだけ理解してください．
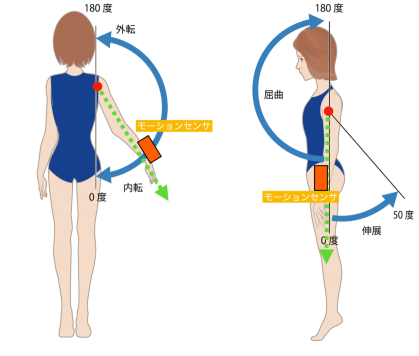
次のページ「モーションセンサを使用した角度の算出方法2」では，直線（Y軸）と水平面のなす角度の具体的な計算方法について述べ，モーションセンサをY軸と一致させるように装着すれば，センサを装着するだけで，図1のように腕の角度を正確に測ることができるようになります．
note記事
単位クォータニオンについてはnote記事「モーションにおける３次元回転」もご参照ください．
参考文献
[1] 広瀬茂男, 「ロボット工学 ー機械システムのベクトル解析ー」，裳華房，東京，pp.142-143，1987
[2] 原文雄，「機械工学」，朝倉書店，東京，pp.87-88，1996