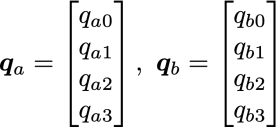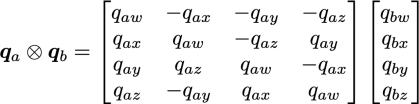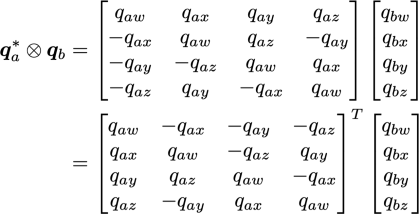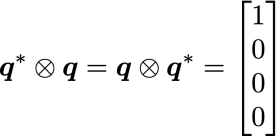クォータニオン4:クォータニオンの演算
クォータニオン(quaternion)は四元数(しげんすう)と呼ばれ,2次元平面の回転を表現する「複素数の拡張」として,3次元の回転を表現することができます.なお,ただのクォータニオンはそれだけでは回転を表現しません.大きさが1という拘束のある単位クォータニオン(オイラーパラメータ)によって回転を表現します.
したがって,クォータニオンで成立する演算が,オイラーパラメータで成立するとは限らないので注意しましょう.
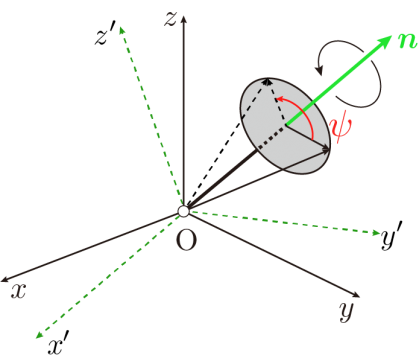
クォータニオンの幾何学的な意味は「ロドリゲスの式からクォータニオンへ」などで述べましたが,ここでは,クォータニオンの演算について,その一部を述べていきます.
なお,以下の性質はオイラーパラメータ(単位クォータニオン)だけでなく,一般的なクォータニオンで成立する性質であるため,ここでは,2つのクォータニオンqaとqb
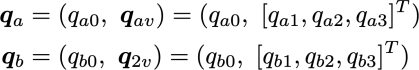
を使いその性質を表していきます.なお,ここでは,スカラ部とベクトル部の形式和を「+」で表す(qa0 + qav)の形式ではなく,上記のような括弧を使った表現方法を便宜上使用します.
クォータニオンを使用した演算(加減乗除,内積,外積も含める)は成立しますが,本項で扱っている回転が成立するオイラーパラメータでも成立する演算として,クォータニオン積,共役クォータニオンを取り上げます.
クォータニオン積
ここで,上付きTの記号はベクトルの転置を表し,a^T b はベクトルaとbの内積を意味します.また一番最後のxの積は,ベクトルの外積の演算子を意味します.このようにスカラ部とベクトル部に分けた計算を行うと,複雑ですが,次のようにクォータニオンを縦ベクトル
で表し,行列を使用してクォータニオン積は
のように書き表せます.この場合,このクォータニオンが回転を表すオイラーパラメータ(単位クォータニオン)である場合,qbの回転を行った次に,回転qaを行う,このクォータニオン積は合成の回転を表しています.なお,クォータにオニオン積は可換ではありません.つまり,回転順番が異なれば,合成の回転は異なり,qa ⊗ qb ≠ qb ⊗ qa となります.
共役クォータニオン
のように,ベクトル部,すなわち回転軸の向きを反対にするのが,共役クォータニオンで,これは回転を表すオイラーパラメータでは逆回転を意味します.
そこで,qa の共役クォータニオンqa*とクォータニオンqbのクォータニオン積は
のように最初の行列の転置行列を用いて記述することができる.したがって,q* ⊗ q は無回転で,
となります.オイラーパラメータ[1, 0, 0, 0]^Tは無回転であることは,ご自身で確かめてください.
そのほかの演算
クォータニオン積以外にも,和と差,内積,外積などの演算がクォータニオンには存在しますが,クォータニオンの和や差は,もはや大きさが1にならないことは容易に想像ができ,オイラーパラメータ(単位クォータニオン)の性質が成り立たないこともわかります.
ここでは,回転,すなわちオイラーパラメータで成立する(大きさ1を維持する)クォータニオンの演算だけ取り上げました.
このように,オイラーパラメータは,オイラー角と異なり,回転の計算はオイラーパラメータ同士の計算で閉じることができ,かつ行列の計算で表現できるところに,線形計算をする上で大きなメリットがあります.
note記事
単位クォータニオンについてはnote記事「モーションにおける3次元回転」もご参照ください.