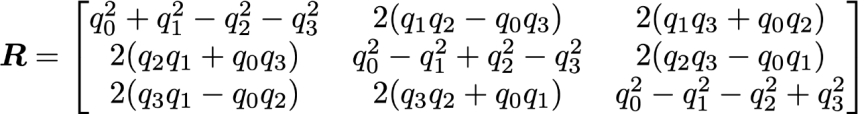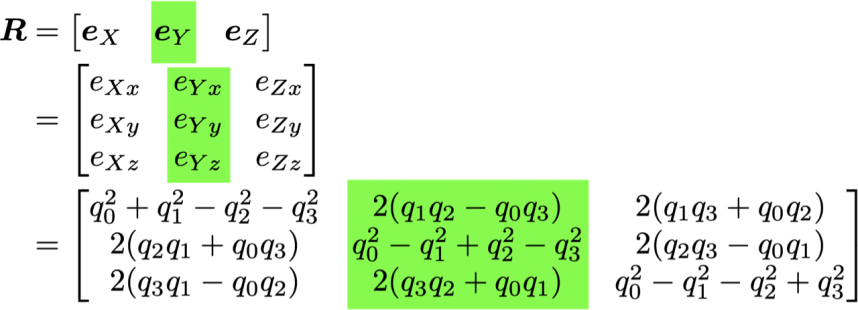モーションセンサを使用した角度の算出方法 その2
直線と平面のなす角度の計算方法
ここでは，具体的にモーションセンサから算出された姿勢角度としてのクォータニオンから，腕などの軸方向の角度を計算する方法を考えていきます．
クォータニオンによる回転行列表現
ページ「モーションセンサを使用した角度の算出方法1」では，「剛体の姿勢角度」と「直線間のなす角度」の違いを述べましたが簡潔に違いを述べると，前者は三つの軸で，後者は一つの軸で角度を表現します．また，直交する三軸をあわらす回転行列 R は物体（剛体）の各座標軸XYZに固定された基底（単位ベクトル） eX, eY, eZを並べたものということも説明しました．
回転行列のクォータニオン表現
一方，「ロドリゲスの式からクォータニオンへ」ではクォータニオン（q0, q1, q2, q3）で回転行列を表現できることを示しました．ここで，再掲しますと，
式（2）
のように書き表すことでできます．このうち真ん中の縦ベクトルが，前のページで説明したように，単位ベクトル eY に相当します．すなわち
式（3）
の緑の部分が，物体に固定されたローカル座標系の eY の絶対座標系における各xyz成分に相当し， eY の絶対座標系における方向がわかったことになります．
そこで，三つの軸で表現される「姿勢角度」から，一つの軸である「直線間のなす角度」（「直線と平面のなす角度」は「直線間のなす角度」に帰着できます）を計算するために，ここでは，三つの軸のうちから緑の eY を選択し，この軸と水平面（xy平面）のなす角度を求めます．
Y軸と水平面のなす角度
図6：eYの各成分と水平面とのなす角度θ
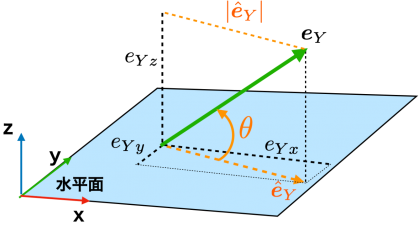
図6のように，単位ベクトル eY の水平面に投影したベクトルをオレンジ色の e^_Y とします．ここでは，記号^（ハットと呼ぶ）のついたベクトルは水平面に投影されたベクトルという意味で使用しています．
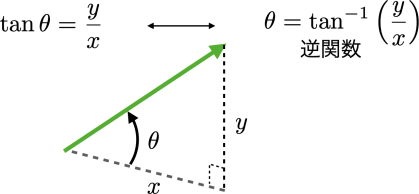
この単位ベクトル eY の水平面になす角度は，緑の単位ベクトル eY とオレンジの投射ベクトル e^_Y のなす角度として，tan()の逆関数を使用することで算出できます．すなわち， e^_Y の大きさ| e^_Y |と，単位ベクトル eY のz成分 e_Yz を使用して，
式（4）
から「水平面となす角度 θ」を計算することができます．
atan2()について
図7
ここで，atan2(y, x)はtan()の逆関数（tan()とは反対に，xとyから角度θを出力する関数）のPythonやC言語などで使用できる組み込み関数で，atan2()は2引数，水平成分xと鉛直y成分をとり，引数の順番が(y, x)となっていることに注意をしてください．
なお，このatan2(y, x)は二つの引数をとることにより，値域が360度の範囲（言語によって，異なります）で符合付きで角度θを算出できますので，逆正接を利用した角度計算では，一引数のatan(y/x)ではなく，二引数のatan2(y,x)を用いましょう．
また，角度を計算する逆関数として他にもacos()やasin()などがありますが，計算精度と定義域からも，acos()やasin()ではなく，やはりatan2()を使用しましょう．角度計算では二つのベクトルの内積を利用してacos()を使用する方が楽ですが，「atan2()を用いることが角度計算の基本」です．
Y軸と水平面のなす角度の計算方法
さて，e^_Y の大きさ| e^_Y | は，ピタゴラスの定理（図6の e_Yx と e_Yy 参照）と，eY を表すクォータニオンの式（3）から
式（5）
となるので，
式（6）
のように，Y軸と水平面のなす角度θを，クォータニオンから計算することができます．なお，この方法の角度の値域は（ーπ/2 ＜θ＜= π/2 ）の180度の範囲となっています．ご注意ください．それ以外の領域の角度を計算するには，e^_Y の大きさ| e^_Y | に加えて，符合が必要となります．
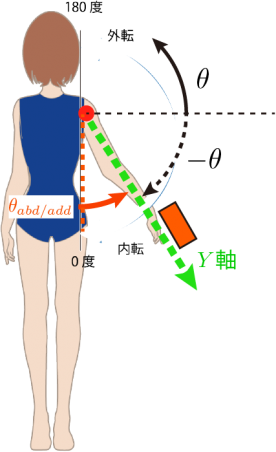
センサを使用した内外転の計測例
最後に，内外転角度を計算する際の補足をします．
図8：センサを使用した内外転の計測例
例えば，前腕と上腕を一直線にしながら内外転運動をしていると仮定し，前腕の長軸方向とセンサのY軸方向を一致させるようにモーションセンサを取り付けます．
すると「水平面と前腕のなす角度：θ」は式（6）のように得られます．しかし，鉛直下方を0度と内外転角度を定義する場合は，水平面と90度（π/2ラジアン）ずれているので，角度θに対して90度を加えることで計算できますので，最終的に内外転角度 θ_{abd/add)は
式（7）
から計算できます．
その他の角度計算について
なお，装着方法をそのままにして運動方向を変えるだけで，「腕の伸展・屈曲角度」も，同じ式で計算できます．
また，絶対座標系におけるxz平面やyz平面（モーションセンサの電源起動時に方位角を0とします）を前額面や矢状面と一致させれば，こらの面に投影したセンサの軸角度も同様に計算することができることが容易にわかると思います．水平面に投影した軸の角度も同様です．
さらに応用すれば，前腕と上腕に装着した二つのモーションセンサからも，「肘関節の伸展屈曲角度」も計算できます．
スポーツセンシング社製モーションセンサを使う場合のTIPS
式(6)の後に，定義域と符合の問題を述べました．すなわち，360度の角度定義域で計算するためには，e^_Y の大きさ| e^_Y | だけでなく，この符合が必要となります．
ところが，XとY軸の方向（ヨー角や方位に相当します）は，センサなどの計測機器の定義や仕様よって異なります．スポーツセンシング社のDSPモーションセンサは，計測開始時のセンサの向きで決まり，計測開始時に方位に相当するヨー角を零として計算します（※ 2021年6月1日時点での仕様です）．
もし，なす角度の定義域を360度で計算したい場合は，この例ですと e_Yxや e_Yy の符合から判断することになりますが，計測開始時が基準となっていて，そのときのセンサの姿勢で符合が決まることに注意してください．
note記事
単位クォータニオンについてはnote記事「モーションにおける３次元回転」もご参照ください．