加速度信号の絶対座標系への座標変換（単位クォータニオンの利用）

座標変換

モーションセンサ（以後，MSと呼ぶ）が計測する加速度信号，角速度信号は，MSに固定されたローカル座標系の信号です．例えば，センサを水平に置くと（Z軸を鉛直方向にすると），センサのZ方向にだけ1Gの加速度が計測されます．その状態から，センサをゆっくり傾けると，センサには重力加速度だけが検出されますが，XYZ各軸に重力加速度の成分が検出されます．このように当たり前ですが，センサはセンサに固定されたセンサ（ローカル）座標系の情報を計測します．

一方，絶対座標系で加速度を観察すると，重力加速度は常に鉛直下向きです．運動の解析では絶対座標系の加速度情報が必要とされることも多々あり，そのためにはセンサ（ローカル）座標系の加速度を絶対座標計へ座標変換する必要があります．

---

---

注意点：MSの加速度信号の符号

「加速度センサの基礎」にも記述してありますが，MSの加速度信号を利用する際に注意点が一つあります．MSの加速度信号の符号は逆向きとなっていますので，そのまま利用せず，符号を反対にして（−１をかける），ご利用ください．これは，加速度センサのチップの仕様で，どのメーカのセンサも物理的に正しい加速度と反対向きの信号を出力するためで，当社のMSもチップの出力をそのまま出力しております．

単位クォータニオン　→　回転行列

座標変換を行うためには，センサの姿勢の情報が必要となります．そのもっとも基本的なものは回転行列ですが，単位クォータニオンやオイラー角も姿勢表現の一つです．これらは回転行列を経由して，変換可能です．

さて，当社のMSは単位クォータニオンを出力します．単位クォータニオン q から回転行列 R(q)は，「モーションセンサを使用した角度の算出方法 その2」の最初の式から計算することができます（この式のq0→qw，q1→qx，q2→qy，q3→qz，のように当社のMSの出力のqw,qx,qy,qzを置き換えてください）．

絶対座標系への変換

ここで，センサをその場で回す作業を行うことを想像してください．その場で回す理由は，並進加速度や向心加速度などの他の加速度を小さくさせて，MSの加速度計にできるだけ純粋に重力加速度だけを検出させるためです．

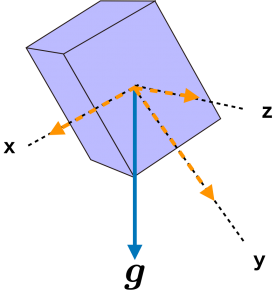
MSを角度θ分回転させることは，加速度計に検出される「重力加速度ベクトル g」を「MSに固定された座標系に座標変換」することに相当します．つまり，MSは重力加速度ベクトル g を， g' = R(-θ) g の計算を通して「センサ座標系」に変換された重力加速度 g' を出力して，図１のように重力加速度1Gをｘｙｚの各成分に分配することになります．

そこで，センサ座標系で計測された加速度をもとの絶対座標系に戻すにはセンサ出力の加速度 a に対して，R(-θ)の逆回転である R(θ) をかければよいので ，単位クォータニオンから計算した回転行列 R(q) と，モーションセンサの加速度 a との積，R(q) a を計算することで絶対座標系に変換できます．

計算の検証方法

単位クォータニオンを使用した上述の方法で正しい計算が行われているかを確認することは簡単です．

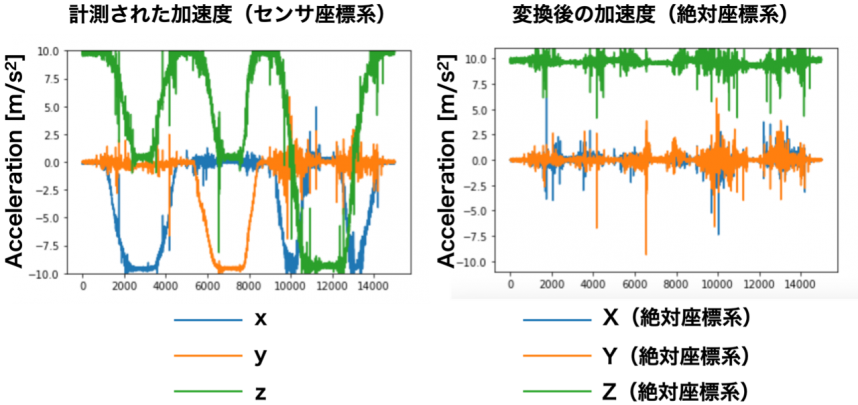
絶対座標系における加速度は，常に鉛直方向（通常z方向）に検出されるので，おおよそ，その場で回転させるようにして計測を行います．その計測された加速度（CSVファイルに出力されます．図２左図参照）を上記の方法で，絶対座標系に絶対変換してください．正しく計算できれば，常にZ方向の加速度が＋１G（=9.8 m/s2)となるはずです（図２右図参照．1kHzサンプリング）．

もし，−１Gとなっている場合は，加速度の符号の補正を忘れています．

---

---

note記事

単位クォータニオンについてはnote記事「モーションにおける３次元回転」もご参照ください．

---