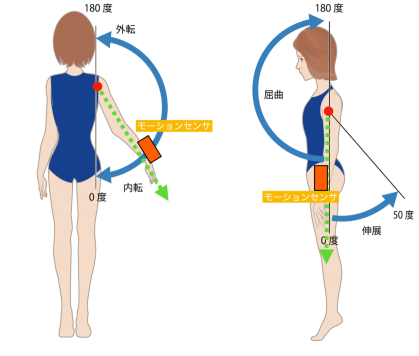
モーションセンサを使用した角度の算出方法 その1
モーションセンサはクォータニオンを初め,オイラー角などの3次元の姿勢角度を出力します.しかし,モーションセンサからクォータニオンが出力されても,実際の角度計測にどのように利用したら良いかわからない方も多いかと思います.
例えば,骨格の線画(スティックピクチャ)の角度をする際に,クォータニオンからそのような角度を計算したいことがあると思いますが,ここではその考え方をご説明いたします.モーションセンサからスティックピクチャを描く際にも,この考え方は役立つはずです.
3次元の姿勢角度の基礎
まず,様々な角度算出を行いたい方のために,その数学的基礎について述べていきます.
なお,最終的な計算方法の結果は次のページで示しますので,以下は読み飛ばしていただいても結構です.
角度と回転
「姿勢」について説明する前に,改めて「角度」と「回転」について整理をしておきたいと思います.