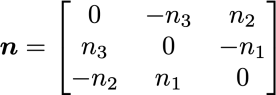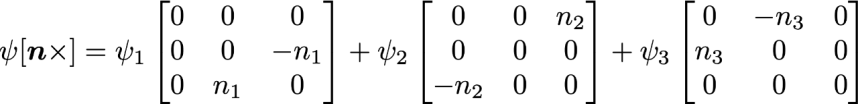クォータニオン2:オイラーの公式からロドリゲスの式へ
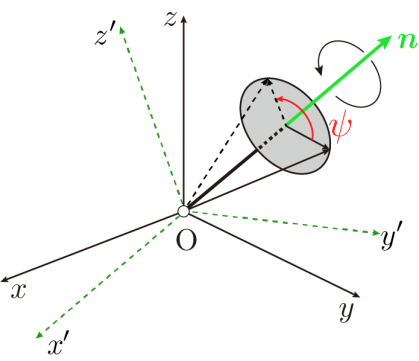
3次元の物体の回転は「ロドリゲスの式」に示したように,ひとつの回転軸 n と回転角度θで表すことができます.
これは,2次元平面の回転を表すオイラーの公式(クォータニオン1:複素数とオイラーの公式)において,複素数に虚数 i をかけることによる,複素平面上で90度の回転に相当します
そこで,このロドリゲスの式が,2次元平面の回転をあわわす「オイラーの公式」
と類似性があることから,これとのアナロジーで3次元の回転を考えます.
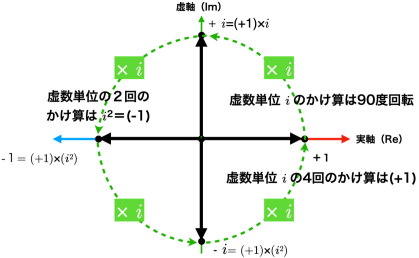
そこで,まず,オイラーの公式(クォータニオン1:複素数とオイラーの公式)で説明した,虚数単位 i をかけることが回転を意味することを示した図を再掲します.
この図のように,(この図では大きさが1の)複素数に虚数 i をかけることは,複素平面上で90度の回転に相当します.
一方,「ロドリゲスの式」
で説明したように,3次元空間における回転を表すこの式も,オイラーの公式と同様に行列を使った指数関数で表現することができます.角度ψを単位回転軸 n まわりに回転させることは,この式では指数関数の中の「ψ[n x]」と記述するだけで良いのですが,これは,まさにオイラーの公式の3次元版を記述していることを暗示しています.
ここで,[n ×]はベクトルnの外積を行列表現したもので,
と表される(座標軸1,2,3軸のそれぞれの成分を, n1, n2, n3とする縦ベクトル)大きさが1の単位ベクトルに対して,
のような歪対称行列(交代行列ともいう)で書くことができます.これは3つの軸成分を持つので,ロドリゲスの式の指数部はさらに
のように分解することもできます.すなわち,第1軸(x軸と考えても良い)回りの回転成分が角度ψ1で,同様に第2,第3軸(y, z軸)成分が,角度ψ2, ψ3となるように分解できます.この分解は,基本的には後述のオイラーパラメータ(単位クォータニオン)でも成立します.
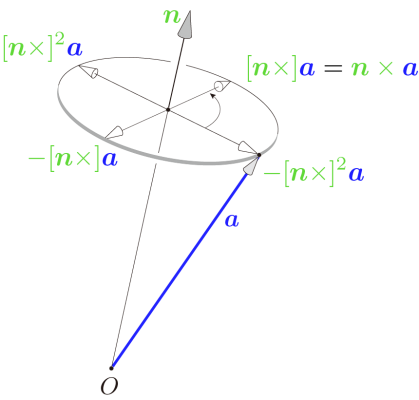
さて,オイラーの公式との類似性を説明する図が次の図
になります.これは,3次元空間のベクトル a に[n x]をかけることで,軸 n 回りに,90度回転することを示しています.ここで,[n x] は軸の単位ベクトル n とベクトル a にたいする外積で,a と n に垂直な方向のベクトルを計算します.これは虚数と同様に,i をかけると90度回転することと同様です.
さらに,もう一度[n x]をかけると,すなわち[n x]^2をかけると,さらに90度回転し,これも虚数i^2=-1となり180度回転することと同じ作用をします.まとめると
i^1 = i, [n x]^1 = [n x]
i^2 = -1, [n x]^2 = [n x] [n x]
i^3 = -i, [n x]^3 = -[n x]
i^4 = 1, [n x]^4 = -[n x]^2
のようになります.以上からロドリゲスの式が,2次元平面の回転を表すオイラーの公式の,3次元への拡張となっていることがわかります.
次に「クォータニオン3:ロドリゲスの式からクォータニオンへ」で,ロドリゲスの式とクォータニオンの関係について述べていき,クォータニオンが3次元の回転を幾何学的に優れた方法であることを示していきます.
note記事
単位クォータニオンについてはnote記事「モーションにおける3次元回転」もご参照ください.