フォースプレートに標準で添付されているアプリケーションで計測されたデータのCSVファイルを用い、重心動揺に関するパラメータ算出を行うアプリケーションのベータ版。
開眼時と閉眼時の計測をそれぞれ行い、比較テーブルを算出することが可能です。。
フォースプレート重心動揺アプリケーション（ベータ版）をダウンロード
※ベータ版の為、算出される値の正確性はございません。
※自己責任でご利用ください。
SKYCOM
DSPワイヤレス9軸モーションセンサーは、センサー内部で加速度/角速度の値から姿勢推定値（クォータニオン）を演算し、その値をメモリ保存できるという優れたハードウェアです。
動作解析を行うことを考えた場合、身体に取り付けられたセンサーの姿勢推定値を、動作解析ソフトウェアへ取り込みたいことがあります。
スポーツセンシング社では、オプティトラック社製のモーションキャプチャシステムを取り扱っており、DSPワイヤレスセンサーや、フォースプレートと共に、モーションキャプチャシステムを同時使用することがあります。
『データコンバータ for SKYCOM』は、姿勢推定によって得られるクォータニオンの値を、SKYCOMの中で剛体として認識するよう、「剛体へ変換するために必要な座標情報を自動的に算出し、かつ、ファイルフォーマットを適切に変換するアプリケーション」です。
DSPワイヤレス9軸モーションセンサ（以降、DSPMS）では、DSPアルゴリズムを入替え可能です。標準では、姿勢推定アルゴリズムを組み込まれており、1kHzサンプリングの慣性センサデータから推定したクォータニオンの値を、無線送信（＋メモリ保存）することが可能です。
スポーツコーチングカム タギングファイル・ユーティリティ
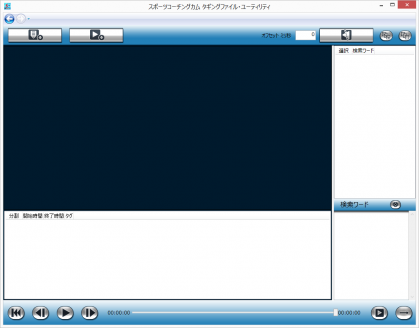
スポーツコーチングカムは、映像を撮影しながらタギング情報を記録できる、他に類をみないビデオカメラです。スポーツセンシング社では、スポーツコーチングカムを最大限に活用していただく為、タギング情報にもとづいて映像の分割を自動的に行ってくれるアプリケーションをご用意しました。
撮影された映像を活用する際に、一番の障害となるのは映像の分割です。これまでは、タギング情報があったとしても、映像編集ソフトウェアを別途用意し、手動で一つ一つの映像切出しを行わなければいけませんでした。
本アプリケーションがあれば、スポーツコーチングカムのタギング情報を元に、長い撮影時間の映像ファイルのから、必要なシーンだけを半自動的に切り出すことが可能です。切出作業の劇的な時間短縮は、試合当日のフィードバックだけなく、選手への映像配布まで実現します。
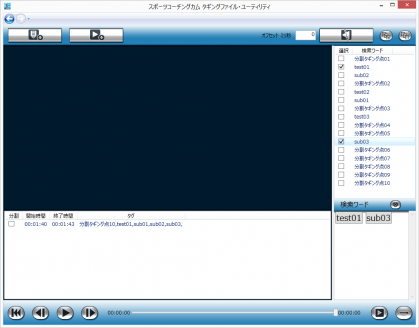
タギング情報の絞り込み
本アプリケーションでは映像ファイルの結合も可能です。
スポーツの現場で必要とされる、以下のようなケースで非常に有用です。
作業が簡単になり、分割機能と組み合わせれば、あっという間にフィードバック映像を作成可能です。
ここでは，具体的にモーションセンサから算出された姿勢角度としてのクォータニオンから，腕などの軸方向の角度を計算する方法を考えていきます．
ページ「モーションセンサを使用した角度の算出方法1」では，「剛体の姿勢角度」と「直線間のなす角度」の違いを述べましたが簡潔に違いを述べると，前者は三つの軸で，後者は一つの軸で角度を表現します．また，直交する三軸をあわらす回転行列 R は物体（剛体）の各座標軸XYZに固定された基底（単位ベクトル） eX, eY, eZを並べたものということも説明しました．
一方，「ロドリゲスの式からクォータニオンへ」ではクォータニオン（q0, q1, q2, q3）で回転行列を表現できることを示しました．ここで，再掲しますと，
式（2）
お電話でのお問い合せはこちら（受付時間 10:00〜18:00）
