クォータニオン1:複素数とオイラーの公式
オイラーパラメータ(単位クォータニオン)は3次元の姿勢や回転を表現する上で,優れた記述方法です.
ここでは,その数学的なアイデアのもととなった,2次元平面の回転を表す複素数とオイラーの公式について,述べていきます.この概念をしっかりと理解しておくことが,オイラーパラメータで回転を計算する上で役立つはずです.
実数の世界
複素数と回転が関係すると言っても,なかなかピンとこないかもしれません.
その前に,ここでは,まず,一直線を表す数直線を示します.
このように数直線は,図の左右の位置を表すことができます.
複素数と複素平面
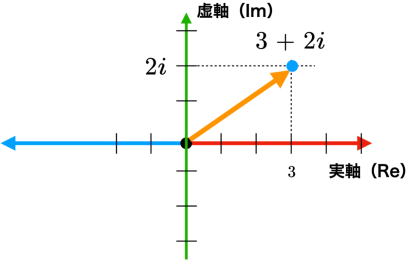
では,次に回転を表現できる複素数とは,なにかというと実部と虚部を足し合わせたものです.例えば,
3+2 i
は,実数で表した実部の3と,実数と虚数 i の積で表す虚部の2 i との和で表しています.上で示した数直線はこの実部に相当します.これを複素平面と呼ばれる,実軸と虚軸の二つの座標軸で表すグラフ表示すると
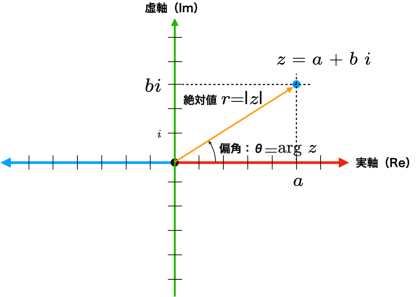
のように描画することができます.これを一般化して,
のように書き表すことができ,回転角度は図に示した偏角で表現できます.
複素数と回転
さて,複素数はこのように,実軸と虚軸に大きさを持つことができますが,回転を考えるだけなら,大きさが1の円を考えるだけですみます.せっかく,複素数の説明をしましたが,以降,大きさが1の単位円に話を絞ります.
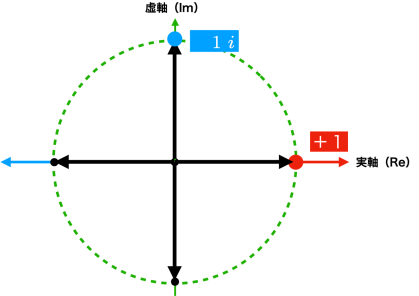
虚部は0で,実部の大きさが+1である複素数をこの単位円上に書くと,
の赤色の点となります.次に,この「1」に虚数 i をかけると,「1 i」 になります.ただし,ここではわかりやすく「1 i 」と書きましたが,ただの「 i 」 と書けば十分です.
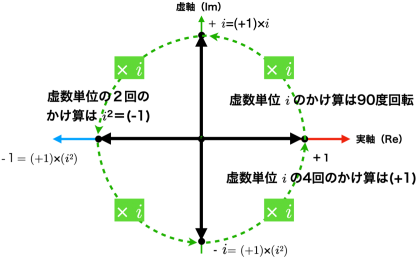
つまり,1に虚数 i をかけることで,複素平面の単位円上を90度回転して,青色の点に移動することになります.つまり,虚数をかけることは,90度回転することに相当します.では,試しに,もう一度 i をかけると,「-1」になります(i * i =-1).複素平面の単位円上をさらに90度回転しています.このように
虚数をかけることが,複素数では回転を表現していることがわかります.
オイラーの公式
この単位円上の回転を数式で表したのが,オイラーの公式です.オイラーの公式は
のように虚数を使用した指数(左辺)と,三角関数と虚数で表した右辺で表現されます.この証明は,他に譲り,右辺に注目します.
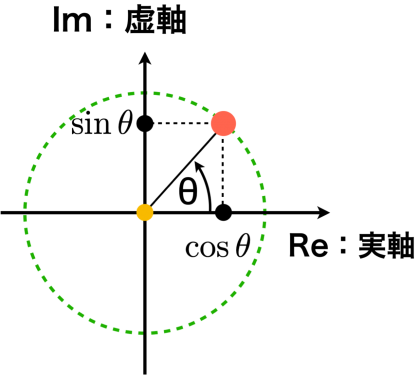
右辺のcosθは実部で,i sinθは虚部であることがわかるので,これは複素数です.この複素数の大きさは,(cosθ)^2+(sinθ)^2ですから,1となっています.ここで,θを前に取り上げた偏角とします.このように
単位円上の点は,偏角θを利用すれば,実部のcosθと,虚部のsinθで表現でき,虚数 i が回転を担っていることを示す,オイラーの公式の右辺を図示することができます.オイラーの公式を用いれば,振動を美しく表現できるなど様々な恩恵がありますが,ここでは,この程度にとどめておきます.詳しい説明は「ブルーバックス,オイラーの公式がわかる」などをご参照ください.
なお「クォータニオン2:オイラーの公式からロドリゲスの式へ」では,このオイラーの公式によって表される2次元平面の回転を,3次元の回転に拡張したロドリゲスの式について説明していきます.
note記事
単位クォータニオンについてはnote記事「モーションにおける3次元回転」もご参照ください.